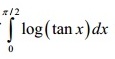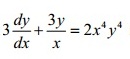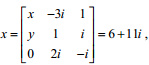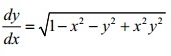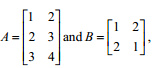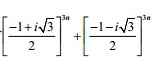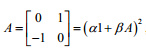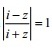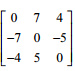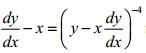JECA - MATHEMATICS
Start
Congratulations - you have completed JECA - MATHEMATICS.
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
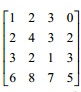
If A be an n × n matrix and C any scalar, then | CA |
A | nC | A | |
B | Cn | A | |
C | nC | A | |
D | C | A | |
Question 2 |
The number of sides of two regular polygons are in the ratio 5 : 4. The difference between their angles is 90. Which one of the following is correct?
A | One of them is a pentagon and the other is a rectangle. |
B | One of them must be a hexagon. |
C | One of them is an octagon. |
D | One of the has 20 sides and the other has 16 sides. |
Question 3 |
The coefficient of the middle term in the expansion of (2 + 3x)4 is
A | 6 |
B | 5! |
C | 8! |
D | 216 |
Question 5 |
The differential of the system of circles touching the y-axis at the origin, is given by
A | x2 + y2 - 2xy dy/dx = 0 |
B | x2 + y2 + 2xy dy/dx = 0 |
C | x2 - y2 + 2xy dy/dx = 0 |
D | x2 - y2 - 2xy dy/dx = 0 |
Question 7 |
A | 1/ x 2 |
B | 1/ x 3 |
C | 1/ x 4 |
D | x 4 |
Question 8 |
The rate at which bacteria multiply is proportional to the instantaneous number present. If the original number doubles in 2 hours, then they will triple in
A | 4 log 2/log 3 hours |
B | 5 log 2/log 3 hours |
C | 2 log 2/log 3 hours |
D | log 2/log 3 hours |
Question 10 |
The number of words that can be formed from the letters of the word INDRAPRASTHA when the vowels are never separated is
A | 727560 |
B | 725760 |
C | 752760 |
D | 757260 |
Question 11 |
The modulus and principle amplitude of (1 + i√3)2 , respectively are
A | 2, - π/2 |
B | 4, 2π/3 |
C | 5/8, tan<>sup>-1(-4/3) |
D | 4, - 3π/4 |
Question 12 |
If 1, ω, ω2 are the cube roots of unity, then value of (x + y)2 to (xω + yω2)2 + (xω2 + yω)2 is equal to
A | xy |
B | 3xy |
C | 6xy |
D | 9xy |
Question 13 |
The number of ways in which 6 people can be seated at a round table is
A | 6 |
B | 60 |
C | 120 |
D | 720 |
Question 14 |
If A ≠ O and both the conditions (i) A.B = A.C (ii) A×B = AxC hold simultaneously, then
A | B=C=0 |
B | B=C |
C | B ≠ C |
D | B ≠ 0 , C ≠ 0 |
Question 16 |
If log8m + log81/6 = 2/3 ,then m is equal to
A | 24 |
B | 18 |
C | 12 |
D | 4 |
Question 17 |
If ax = by = cz ,and logba = logcb ,then which one of the following will hold true?
A | y2 = xz |
B | x2 = yz |
C | z2 = xy |
D | y = xz |
Question 18 |
The area bounded by the coordinate axes and the curve √x + √y = 1 is equal to ?
A | 1 |
B | 1/2 |
C | 1/3 |
D | 1/6 |
Question 19 |
If(x - 2)(x +6 ) ≥ 0, then the solution set is
A | (x:x ≥ 2) |
B | (x:x ≤ 6 ) |
C | (x:x ≤ -6 ) |
D | (x:x ≥ 2 or x ≤ -6 ) |
Question 20 |
The the mth and the nth terms of an H.P. are n and m respectively, then the mnth term is
A | 0 |
B | 1 |
C | 2 |
D | 1/2 |
Question 22 |
The value of tan 31o .tan 32o .tan 32o .tan 33o ...tan 59o is equal to
A | -1 |
B | 0 |
C | 1 |
D | 2 |
Question 23 |
A | A2 + AB + BA + B2 |
B | A2 + 2AB + B2 |
C | A2 + AB + BA + B2I |
D | A2I + AB + BA + B2 |
Question 24 |
The value of 3 - 1 + 1/3 - 1/9 =..... is equal to
A | 20/9 |
B | 9/20 |
C | 9/4 |
D | 4/9 |
Question 25 |
If in the binomial expansion of (1 + x)n when n is a natural number, the coefficients of the 5th, 6th and 7th terms are in A.P., then n is equal to
A | 7 or 13 |
B | 7 or 14 |
C | 7 or 15 |
D | 7 or 17 |
Question 26 |
A | sin-1 y - sin-1 x + c |
B | sin-1 y = 1/2 √1 - x2 + 1/2sin-1 x + c |
C | sin-1 y = 1/2x √1 - x2 + 1/2sin-1 x + c |
D | sin-1 y = 1/2x √1 - x2 + 1/4cos-1 x + c |
Question 28 |
The binary number 10110100001 in decimal system is
A | 441 |
B | 1441 |
C | 1241 |
D | 241 |
Question 29 |
The binary number 1101101 + 1011011 is written in decimal system as
A | 198 |
B | 199 |
C | 200 |
D | 201 |
Question 30 |
The solution of equations 3x + y + 2z = 3; 2x - 3y - z = -3 and x + 2y + z = 4 is
A | x= 3 , y= 2 , z= -2 |
B | x= 2 , y= 1 , z= 3 |
C | x= 1 , y= 2 , z= -1 |
D | x= 1 , y= 2 , z= 1 |
Question 31 |
In a Euclidean plane, which one of the following is not an equivalence relation?
A | Parallelism of lines (a line being deemed parallel to itself) |
B | Congruence of triangles |
C | Similarity of triangles |
D | Orthogonality of lines |
Question 32 |
There are 600 students in a school, If 400 of them can speak Telugu, 300 can speak Hindi, then the number of students who can speak both Telugu and Hindi are
A | 100 |
B | 200 |
C | 300 |
D | 400 |
Question 33 |
A | both AB and BA exist |
B | neither AB nor BA exists |
C | AB exists but BA does not exists |
D | AB does not exist but BA exist |
Question 34 |
If b→ is a unit vector in the xy-plane making an angle of π/4 with the x-axis, then b→ is equal to
A | iˆ + jˆ |
B | iˆ - jˆ |
C | (iˆ + jˆ) / √2 |
D | (iˆ - jˆ) / √2 |
Question 36 |
A | x - 3 |
B | x - y |
C | y - 3 |
D | (x - 3)(y - 3) |
Question 37 |
A | α = 1/√2 , β = 1/√2 |
B | α = -1/√2 , β = 1/√2 |
C | α = β = ±1/√2 |
D | α = -β = ±1/√2 |
Question 38 |
A | a circle with the centre (0, 0) and radius 1 |
B | the x-axis |
C | the y-axis |
D | the line y = x + 1 |
Question 40 |
y – A cos ωt + B sin ωt is a solution of the differential equation
A | d2y / dt2 - ω2y = 0 |
B | d2y / dt2 - ωy = 0 |
C | d2y / dt2 + ωy = 0 |
D | d2y / dt2 + ω2y = 0 |
Question 41 |
The number of 2-digit even numbers that can be formed from the digits 1, 2, 3, 4 and 5, repetition being not allowed, is
A | 25 |
B | 5! |
C | 16 |
D | 8 |
Question 42 |
If the equations x2 −px +q = 0 and x2 +qx -p = 0 have a common root, then which one of the following will hold true?
A | p = q |
B | p + q = 2 |
C | p + q = 1 |
D | p – q = 1 |
Question 43 |
The general solution of dy/dx + y = sin x is
A | y = ce-2x + 1/4 sin x - 1/2 cos x |
B | y = ce-x + 1/2 sin x - 1/2 cos x |
C | y = ce-3x + sin x |
D | y = ce-x |
Question 44 |
If (x + 1/x) = 3 , then (x6 + 1/x6) is equal to
A | 927 |
B | 414 |
C | 364 |
D | 322 |
Question 46 |
Distance between two points whose position vectors are 3iˆ + jˆ - 2kˆ and iˆ - 3jˆ + 5kˆ
A | 69 units |
B | √69 units |
C | 13 units |
D | 29 units |
Question 47 |
The binary equivalent to the decimal number 0.3125
A | 0101 |
B | .1010 |
C | .0101 |
D | .1101 |
Question 48 |
α, β, ξ, η are non-empty sets then
A | (α x β) ∪ (ξ x η) = (α x β) ∩ (ξ x η) |
B | (α x β) ∩ (ξ x η) = (α x ξ) ∩ (β x η) |
C | (α x β) x (ξ x η) = (α x ξ) ∪ (β x η) |
D | (α x β) x (ξ x η) = (α x η) ∪ (β x ξ ) |
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
Get Results
There are 50 questions to complete.
← |
List |
→ |
Return
Shaded items are complete.
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 |
| 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 |
| 46 | 47 | 48 | 49 | 50 |
| End |
Return
You have completed
questions
question
Your score is
Correct
Wrong
Partial-Credit
You have not finished your quiz. If you leave this page, your progress will be lost.
Correct Answer
You Selected
Not Attempted
Final Score on Quiz
Attempted Questions Correct
Attempted Questions Wrong
Questions Not Attempted
Total Questions on Quiz
Question Details
Results
Date
Score
Hint
Time allowed
minutes
seconds
Time used
Answer Choice(s) Selected
Question Text
All done
Need more practice!
Keep trying!
Not bad!
Good work!
Perfect!