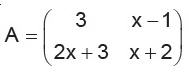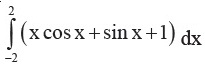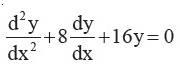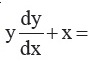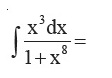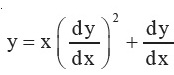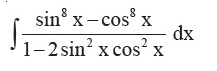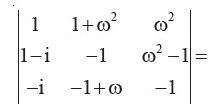WBJEE (Mathematics) Model Test

WBJEE - MATHEMATICS

Please wait while the activity loads.
If this activity does not load, try refreshing your browser. Also, this page requires javascript. Please visit using a browser with javascript enabled.

If loading fails, click here to try again

Number of Questions : 40
Time : 60 Minutes
No negative marking.

Start

Congratulations - you have completed WBJEE - MATHEMATICS. You scored %%SCORE%% out of %%TOTAL%%. Your performance has been rated as %%RATING%%

Your answers are highlighted below.

Question 1

The eccentricity of the hyperbola 4x² – 9y² = 36 is

A	√11/3
B	√15/3
C	√13/3
D	√14/3

Question 2

The length of the latus rectum of the ellipse 16x² + 25y² = 400 is

A	5/32 unit
B	16/5 unit
C	32/5 unit
D	5/16 unit

Question 3

The vertex of the parabola y² + 6x – 2y + 13 = 0 is

A	(3/2,1)
B	(-7/2,1)
C	(1, –1)
D	(–2, 1)

Question 4

The coordinates of a moving point p are (2t² + 4, 4t + 6). Then its locus will be a

A	parabola
B	circle
C	ellipse
D	straight line

Question 5

The equation 8x² + 12y² – 4x + 4y – 1 = 0 represents

A	an ellipse
B	a circle
C	a parabola
D	a hyperbola

Question 6

If the straight line y = mx lies outside of the circle x² + y² – 20y + 90 = 0, then the value of m will satisfy

A	\|m\| > 3
B	m > 3
C	m < 3
D	\|m\| < 3

Question 7

The locus of the centre of a circle which passes through two variable points (a, 0), (–a, 0) is

A	x = 0
B	x + y = a
C	x + y = 2a
D	x = 1

Question 8

The coordinates of the two points lying on x + y = 4 and at a unit distance from the straight line 4x + 3y = 10 are

A	(5, 3), (–1, 2)
B	(3, 1), (7, 11)
C	(3, 1), (–7, 11)
D	(–3, 1), (7, 11)

Question 9

The intercept on the line y = x by the circle x² + y² – 2x = 0 is AB. Equation of the circle with AB as diameter is

A	(x –1)(x–2)+(y–1)+(y–2)= 0
B	x² + y² = 1
C	x(x – 1) +y(y – 1) = 0
D	x² + y² = 2

Question 10

If the coordinates of one end of a diameter of the circle x²+y²+4x–8y+5=0, is (2,1), the coordinates of the other end is

A	(7, –6)
B	(–6, 7)
C	(6, 7)
D	(–6, –7)

Question 11

If the three points A(1,6), B(3, –4) and C(x, y) are collinear then the equation satisfying by x and y is

A	13x –5y +5 = 0
B	5x + 13y + 5 = 0
C	5x + y – 11= 0
D	5x –13y + 5 = 0

Question 12

If sin θ= 2t/1+t² and θ lies in the second quadrant, then cos θ is equal to

A	t²-1/1+t²
B	-\|1-t²\|/1+t²
C	1-t²/1+t²
D	1+t²/\|1-t²\|

Question 13

The solutions set of inequation cos^–1x < sin^–1x is

A	[0, 1]
B	[–1, 1]
C	(1/√2,1]
D	[1/√2,1]

Question 14

The number of solutions of 2sinx + cos x = 3 is

A	2
B	infinite
C	1
D	No solution

Question 15

Let tan α = a/a+1 and tan β = 1/2a+1 then α + β is

A	π/3
B	π/2
C	π/4
D	π

Question 16

If θ + φ = π/4, , then (1+ tan θ)(1+ tan φ) is equal to

A	1
B	2
C	5/2
D	1/3

Question 17

If sin θ and cos θ are the roots of the equation ax² – bx + c = 0, then a, b and c satisfy the relation

A	a² + b² + 2ac = 0
B	a² + c² + 2ab = 0
C	a² - b² - 2ac = 0
D	a² - b² + 2ac = 0

Question 18

If A and B are two matrices such that A+B and AB are both defined, then

A	A, B are square matrices of the same order
B	Number of columns of A = number of rows of B
C	A and B can be any matrices
D	A, B are square matrices not necessarily of the same order

Question 19

If

is a symmetric matrix, then the value of x is

A	4
B	3
C	-3
D	-4

Question 20

If

then (i = √−1)

A	z is purely imaginary
B	z is purely real
C	z + ‾ z = 0
D	(z - ‾ z ) i is purely imaginary

Question 21

The equation of the locus of the point of intersection of the straight lines x sin θ + (1 – cos θ) y = a sin θ and x sin θ – (1 + cos θ) y + a sin θ = 0 is

A	y ± ax
B	x² + y² = a²
C	y² = 4x
D	x = ± ay

Question 22

If sinθ + cosθ = 0 and 0 < θ < π, then θ

A	π/4
B	3π/4
C	π/2
D	0

Question 23

The value of cos 15° - sin 15° is

A	1/2√2
B	0
C	1/√2
D	-1/√2

Question 24

The period of the function f(x) = cos 4x + tan 3x is

A	π
B	π/2
C	π/3
D	π/4

Question 25

If y = 2x³ – 2x² + 3x – 5, then for x = 2 and Δ x = 0.1 value of Δ y is

A	2.002
B	0.9
C	0
D	1.9

Question 26

The approximate value of ^⁵√33 correct to 4 decimal places is

A	2.0125
B	2.0500
C	2.1001
D	2.0000

Question 27

The value of

is

A	0
B	2
C	-2
D	4

Question 28

For the function f(x)=e^cosx , Rolle’s theorem is

A	applicable when 0 ≤ x ≤ π
B	applicable when 0 ≤ x ≤ π/2
C	applicable when π/2 ≤ x ≤ 3π/2
D	applicable when π/4 ≤ x ≤ π/2

Question 29

The general solution of the differential equation

is

A	(A + Bx)e^–4x
B	(A + B x)e^5x
C	(A + Bx²)e^4x
D	(A + Bx⁴)e^4x

Question 30

If x² + y² = 4, then,

A	1
B	4
C	0
D	-1

Question 31

A	x + 4 tan^–1 x⁴ + c
B	4 tan^–1 x³ + c
C	x² + 1/4 tan ^–1 x⁴ + c
D	1/4 tan ^–1 x⁴ + c

Question 32

A	28
B	0
C	30
D	32

Question 33

The degree and order of the differential equation

are respectively

A	1, 4
B	1,1
C	2, 1
D	4, 1

Question 34

The function f (x) is

A	not continuous at x = 0 and so it is not increasing when x > 0
B	Strictly increasing at x = 0
C	increasing when x ≥ 0
D	strictly increasing when x > 0

Question 35

The function f(x) = ax + b is strictly increasing for all real x if

A	a ≤ 0
B	a = 0
C	a < 0
D	a > 0

Question 36

A	2 sin x + log \|sec x – tan x\| + C
B	2 sin x – log \|sec x – tan x\| + c
C	2 sin x – log \|sec x + tan x\| + C
D	2 sin x + log \| sec x + tan x \| + C

Question 37

A	-1/2 sin 2x + c
B	-1/2 sin x + c
C	1/2 sin x + c
D	1/2 sin 2x + c

Question 38

The general solution of the differential equation log_e (dy/dx) =x + y is

A	e^–x + e^–y = C
B	e^x + e^{y^{= C}}
C	e^x + e^–y = C
D	e^y + e^–x = C

Question 39

If y = A/x + Bx² , then x ² d ² y/d x ²

A	y⁴
B	y³
C	2y
D	y²

Question 40

If one of the cube roots of 1 be ω, then

A	0
B	i
C	ω
D	1

Once you are finished, click the button below. Any items you have not completed will be marked incorrect. Get Results

There are 40 questions to complete.

←

List

→

Return

Shaded items are complete.

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	20
21	22	23	24	25
26	27	28	29	30
31	32	33	34	35
36	37	38	39	40
End

Return

A	2 sin x + log \|sec x – tan x\| + C
B	2 sin x – log \|sec x – tan x\| + c
C	2 sin x – log \|sec x + tan x\| + C
D	2 sin x + log \| sec x + tan x \| + C

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	20
21	22	23	24	25
26	27	28	29	30
31	32	33	34	35
36	37	38	39	40
End

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	20
21	22	23	24	25
26	27	28	29	30
31	32	33	34	35
36	37	38	39	40
End

WBJEE (Mathematics) Model Test

WBJEE - MATHEMATICS

Categories

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	20
21	22	23	24	25
26	27	28	29	30
31	32	33	34	35
36	37	38	39	40
End